iTHEMS数学セミナー
117 イベント
-
セミナー
Ubiquity of geometric Brascamp--Lieb data
2025年2月21日(金) 15:00 - 17:00
辻 寛 (埼玉大学 大学院理工学研究科 日本学術振興会 特別研究員 PD)
This talk is based on a joint work with Neal Bez (Nagoya university) and Anthony Gauvan (Saitama university). The Brascamp--Lieb inequality is a futher general inequality involving some data (we call it the Brascamp--Lieb datum), which has been studied in harmonic analysis and convex geometry. For instance, the Hölder inequality and the Young convolution inequality are particular cases. In this talk, we have an interest in geometric Brascamp--Lieb data, which are specific data satisfying nice properties, for which the best constant of the Brascamp--Lieb inequality is well-understood. Our goal in this talk is to show that geomtric Brascamp--Lieb data are dense in general Brascamp--Lieb data in certain sence. Our result substantially follows from the work by Garg, Gurvits, Oliveira and Wigderson.
会場: セミナー室 (359号室) 3階 359号室とZoomのハイブリッド開催
イベント公式言語: 英語
-
セミナー
The Topology, Geometry and Physics of non-Hausdorff manifolds
2025年2月19日(水) 15:00 - 17:00
O'Connell David (沖縄科学技術大学院大学 (OIST) 博士課程)
Non-Hausdorff manifolds are manifolds containing "doubled points" that cannot be separated by disjoint open sets. In this talk we will survey some mathematical and physical results surrounding these unusual spaces. As a theme, we will start with their fundamental description as a topological space, and slowly add in more and more structure of interest until we can meaningfully phrase questions of physics. On the mathematical side, we will see descriptions of non- Hausdorff manifolds as colimits of ordinary manifolds, which allows us to describe their geometric features without appealing to arbitrarily- existent partitions of unity. On the physical side, we will consider the inclusion of non-Hausdorff manifolds in a naïve 2d Lorentzian path integral for gravity, and (time permitting) explain how construct quantum fields on a non-Hausdorff background. Ultimately, we will see that these latter two arguments suggest that non-Hausdorff manifolds may be more appropriate than the standard "Trousers space" for the modelling of topology change in Lorentzian signature.
会場: セミナー室 (359号室) 3階 359号室とZoomのハイブリッド開催
イベント公式言語: 英語
-
セミナー
Operator-algebraic approach to point processes
2025年2月14日(金) 15:00 - 17:00
佐藤 僚亮 (中央大学 理工学部 学振特別研究員PD)
A point process is a mathematical description of a particle system with random interactions, and it naturally appears in various areas of mathematical physics and mathematics, including statistical mechanics, random matrix theory, combinatorics, and representation theory. In particular, a random particle system with repulsive interactions is associated with a determinantal point process, in which the correlation of any number of particles is expressed in terms of the two-particle correlation via a determinant. Furthermore, this determinantal structure enables an algebraic analysis using CAR algebras, which are operator algebras determined by canonical anti-commutation relations. In the first half of the talk, we will review the relationship between determinantal point processes and operator algebras, with a focus on why operator algebras naturally lend themselves to analyses in probability theory and statistical mechanics. In the second half, based on recent work, we will examine the dynamic relationship between point processes and operator algebras, discussing how dynamics on CAR algebras give rise to stochastic processes on determinantal point processes.
会場: セミナー室 (359号室) (メイン会場) / via Zoom
イベント公式言語: 英語
-
セミナー
D-modules and the Riemann-Hilbert correspondence as a foundation for mixed Hodge modules
2025年1月31日(金) 14:00 - 16:00
齋藤 隆大 (中央大学 理工学部 助教)
Algebraic analysis is a field which began with the study of differential equations in an algebraic framework, known as D-modules. The Riemann-Hilbert correspondence lies at the heart of this field, which bridges the worlds of analysis and geometry. Thanks to this, some geometric problems can be studied by using D-module theory, and vice versa. Based on D-module theory, Morihiko Saito introduced the concept of mixed Hodge modules, realizing Hodge theory on constructible sheaves, which brings us a functorial treatment of Hodge theory and various applications. In this talk, we will begin with the linear differential equations on the complex plane and introduce monodromy, regularity and Deligne's Riemann-Hilbert correspondence. Then, as a generalization of it, I will explain the basics of the theory of D-modules and the Riemann-Hilbert correspondence. Finally, I will describe the role they play in the theory of Hodge modules and recent progress in this area. For the audience's background knowledge, I will assume basic complex function theory. I will start with a simple example, so people outside the field are welcome.
会場: セミナー室 (359号室) (メイン会場) / via Zoom
イベント公式言語: 英語
-
セミナー
Probabilistic approach to discrete integrable systems
2025年1月17日(金) 15:30 - 17:30
佐々田 槙子 (東京大学 大学院数理科学研究科・理学部数学科 教授)
The KdV equation and the Toda lattice are two central and widely studied examples of classical integrable systems, and many of their variations have been introduced to the present. In particular, the box-ball system (BBS) is a basic example of a discrete integrable system, which has been revealed to be an ultra-discrete version of the KdV equation and the Toda lattice. The BBS has been studied from various viewpoints such as tropical geometry, combinatorics, and cellular-automaton. As a new perspective, research on probabilistic approaches to this system has been rapidly expanding in recent years, including the application of the Pitman transform, analysis of invariant measures and its generalized hydrodynamics. More recently, we find that the application of the Pitman transform and the study of invariant measures of i.i.d.-type also work in the same manner for the discrete KdV equation and the discrete Toda lattice. Further research has begun on the relationship between the Yang-baxter maps and the existence of i.i.d.-type invariant measures for the discrete integrable systems. In this talk, I will introduce these new research topics that have been spreading over the past several years from the basics. This talk is based on several joint works with David Croydon, Tsuyoshi Kato, Satoshi Tsujimoto, Ryosuke Uozumi, Matteo Mucciconi, Tomohiro Sasamoto, Hayate Suda and Stefano Olla.
会場: セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Recent Advances in the Spectral Geometry of Domains and Approaches with Computer-Assisted Proofs
2024年12月12日(木) 15:00 - 17:00
遠藤 凌輝 (新潟大学 大学院自然科学研究科 数理物質科学専攻 博士課程)
What can we determine about the shape of a drum from its sound?"—This inverse problem has given rise to spectral geometry and has attracted researchers for over 110 years. The first half of the talk explains recent advances in shape optimization problems for domains with respect to eigenvalues of the Laplacian and the inverse problem known as "hearing the shape of a drum," presented in an accessible manner for experts from other disciplines. The second half introduces verified computation methods for eigenvalues, eigenfunctions, and shape derivatives. As applications, it presents newly established computer-assisted proofs for the minimization problem of eigenvalues with non-homogeneous Neumann boundary conditions, and the conjecture on the simplicity of the second Dirichlet eigenvalues for non-equilateral triangles.
会場: セミナー室 (359号室) (メイン会場) / via Zoom
イベント公式言語: 英語
-
セミナー
Young's convolution inequality on locally compact groups
2024年10月18日(金) 15:00 - 17:00
里見 貴志 (理化学研究所 数理創造プログラム (iTHEMS) 基礎科学特別研究員)
Young's convolution inequality is one of the elementary inequalities in functional and harmonic analysis, and this inequality is related to various theories in mathematics, physics, and computer theory. In addition, it is known that Young's inequality can be generalized to any locally compact group. In this talk, we introduce the definition of locally compact groups and the statement of Young's inequality with several examples. Finally, we see the speaker's recent results about refining Young's inequality for several locally compact groups, including the special linear groups.
会場: セミナー室 (359号室) (メイン会場) / via Zoom
イベント公式言語: 英語
-
セミナー
Topological recursion and twisted Higgs bundles
2024年7月16日(火) 10:30 - 12:00
Christopher Mahadeo (Research Assistant Professor, Department of Mathematics, The University of Illinois at Chicago (UIC), USA)
Prior works relating meromorphic Higgs bundles to topological recursion have considered non-singular models that allow the recursion to be carried out on a smooth Riemann surface. I will discuss some recent work where we define a "twisted topological recursion" on the spectral curve of a twisted Higgs bundle, and show that the g=0 components of the recursion compute the Taylor expansion of the period matrix of the spectral curve, mirroring a result of for ordinary Higgs bundles and topological recursion. I will also discuss some current work relating topological recursion to a new viewpoint of quantization of Higgs bundles.
会場: セミナー室 (359号室) (メイン会場) / via Zoom
イベント公式言語: 英語
-
セミナー
On the volume conjecture for the Teichm ̈uller TQFT
2024年5月31日(金) 15:00 - 17:00
上村 宗一郎 (東京大学 大学院数理科学研究科 博士課程)
The Chern-Simons theory is a topological quantum field theory (TQFT) on the principal G-bundle and has been studied in both mathematics and physics. When G is SU(2), which is compact, Witten conjectured that its path integral gives the topological invariant of the base 3-manifold. This invariant was formulated rigorously and is known as the WRT invariant. In addition, it is known that the expectation value of the Wilson loop along the hyperbolic knot in S3 gives the invariant of knots, which is called the colored Jones polynomial. Invariants of knots and manifolds derived from the path integral are called quantum invariants. There is an open conjecture called the volume conjecture, which states that the complete hyperbolic volume of the knot complement appears in the asymptotic expansion of the colored Jones polynomial. The volume conjecture suggests a close connection between quantum invariants and hyperbolic geometry. On the other hand, Chern-Simons theory with the non-compact G such as SL(2,C) also appears in duality in string theory called the 3d-3d correspondence but has not been well formulated mathematically. Andersen and Kashaev constructed a TQFT-like theory called the Teichm ̈uller TQFT by quantizing the Teichm ̈uller space, which is the deformation space of the hyperbolic structures on a surface. The Teichm ̈uller TQFT is expected to correspond to the SL(2,C) Chern-Simons theory. In this theory, a conjecture similar to the volume conjecture has been proposed and proven for several hyperbolic knots. In this talk, I will introduce the outline of the Teichm ̈uller TQFT and explain our results on the volume conjecture and its proof using techniques in hyperbolic geometry by Thurston, Casson, Rivin, and others.
会場: via Zoom / セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Introduction to homotopy theory
2024年5月24日(金) 15:00 - 17:00
小泉 淳之介 (理化学研究所 数理創造プログラム (iTHEMS) 基礎科学特別研究員)
In a narrow sense, homotopy theory is a framework for capturing the essential structures of shapes and has long been used as a powerful tool in topology. On the other hand, the concept of homotopy is so universal that it appears even in purely algebraic settings and has recently had a significant impact on other fields such as number theory and algebraic geometry. This talk aims to introduce homotopy theory in this broader sense from multiple perspectives. If time permits, I will also touch upon recent developments in the homotopy theory of algebraic varieties.
会場: via Zoom / セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Introduction to operator algebras
2024年5月17日(金) 15:00 - 17:00
北村 侃 (理化学研究所 数理創造プログラム (iTHEMS) 基礎科学特別研究員)
I will give a quick introduction to operator algebras. Operator algebras in this talk consist of linear operators over some Hilbert space. Their study was initiated by Murray and von Neumann, motivated partially by the mathematical foundation of quantum mechanics. Starting from the definitions of a few basic notions, I will explain that commutative operator algebras can be interpreted as spaces. On the other hand, simple operator algebras (i.e., those without non-trivial ideals) form a class of operator algebras opposite to commutative ones and have attracted many operator algebraists. I will try to introduce several examples of simple operator algebras, some of which appear in mathematical physics. If time permits, I will also give recent results on ideals in C*-algebras. People with any scientific background are welcome.
会場: via Zoom / セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Knot Theory in Doubly Periodic Tangles and Applications
2024年1月19日(金) 15:00 - 16:30
ソニア・マムーディ (東北大学 材料科学高等研究所 (AIMR) 数学連携グループ 助教)
Doubly periodic entangled structures offer an interesting framework for modeling and investigating diverse materials and physical phenomena, from micro to large scales. Specifically, a doubly periodic tangle (DP tangle) is characterized as an embedding of an infinite number of curves in the thickened plane, derived as the lift of a link in the thickened torus to the universal cover. DP tangles play a crucial role in scientific research, particularly in fields such as materials science, molecular chemistry, and biology. Despite their widespread applications, a universally accepted mathematical description of DP tangles is currently lacking. One of the key challenges arises from the infinite possibilities in choosing a periodic cell (referred to as a motif) for a DP tangle, taking into account various periodic boundary conditions. In this presentation, we conduct a comprehensive examination of the concept of topological equivalence of DP tangles, offering insights into potential classifications and applications in the process.
会場: 研究本館 3階 359号室とZoomのハイブリッド開催
イベント公式言語: 英語
-
セミナー
Tropical geometry and period integrals
2023年12月13日(水) 14:00 - 16:30
山本 悠登 (理化学研究所 数理創造プログラム (iTHEMS) 基礎科学特別研究員)
Tropical geometry is a field of mathematics that naturally emerges when considering the limits of spaces with respect to some parameters. One of the motivations to study tropical geometry is to describe the behaviors of the spaces under the limit. In this math seminar, starting with a brief introduction to tropical geometry, we discuss its application to computation of period integrals, which are one of the most fundamental quantities of complex manifolds. The goal is to compute asymtptotics of period integrals for complex hypersurfaces in toric varieties using tropical geometry, and observe that the Riemann zeta values (or the gamma classes) appear in the result of the computation. The first half of the talk will be a brief introduction to tropical geometry for non-experts including those who are working outside mathematics, and everyone will be welcome.
会場: 研究本館 3階 359号室とZoomのハイブリッド開催
イベント公式言語: 英語
-
セミナー
Introduction and prospects of topological recursion
2023年11月17日(金) 15:00 - 17:00
大須賀 けん斗 (東京大学 大学院数理科学研究科 日本学術振興会 特別研究員 PD)
Topological recursion is a universal recursive formalism that connects many branches in mathematical physics, such as enumerative geometry, algebraic geometry, integrable hierarchy, matrix models, 2d gravity, and more. In the first half of this talk, I will give a pedagogical overview of topological recursion and present simple examples from which we learn how topological recursion works. Then in the second half, I will present some ongoing research projects as well as a few future directions in topological recursion.
会場: セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Geometry of special nilpotent orbits
2023年11月15日(水) 14:00 - 15:30
Baohua Fu (Professor, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, China)
Special nilpotent orbits play a key role in representation theory, but their geometry is little understood. I'll first report a joint work with Yongbin Ruan and Yaoxiong Wen proposing a mirror symmetry conjecture for special nilpotent orbits and then a joint work with Daniel Juteau, Paul Levy and Eric Sommers on the proof of sliced version of Lusztig's conjecture on special pieces.
会場: via Zoom
イベント公式言語: 英語
-
セミナー
A cluster algebra structure in the quantum cohomology ring of a quiver variety
2023年10月24日(火) 10:00 - 11:30
Yingchun Zhang (Postdoctoral Researcher, Institute for Advanced Study in Mathematics, Zhejiang University, China)
The Gromov-Witten theory of a quiver variety is expected to be preserved by quiver mutation according to Seiberg duality, which has been proved to be true for A-type and star-shaped quivers. Cluster algebra can be constructed for a given quiver via quiver mutation. The two subjects Gromov-Witten and cluster algebra seem to differ a lot. Howerver, when we move to the quantum cohomology ring of a quiver variety, Benini-Park-Zhao’s work “indicates” that there should be a cluster algebra structure in the quantum cohomology ring of the quiver variety. In this talk, I will introduce our recent work about the construction of such a cluster algebra structure in the quantum cohomology of a quiver variety. In particular, we will give a proof of the construction for A-type cluster algebra in quantum cohomology of a flag variety. This is a joint work with Weiqiang He.
会場: セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Interactions between Algebraic Topology and Representation Theory by Toric Code
2023年10月2日(月) - 4日(水)
ミンキュ・キム (Research Fellow, School of Mathematics, Korea Institute for Advanced Study (KIAS), Republic of Korea)
Toric code is an error correction code designed by Kitaev in late 1990’s, which contributes to the birth of topological quantum computation. The goal of these lectures is to introduce toric code and related mathematics. We will explain an interaction between low-dimensional topology and representation of Drinfeld double. Especially, we will encode several operations (e.g. braidings) on representations into topology and geometry on surfaces. If time allows, we will give an overview of how toric code arises from chain complexes, which will be the prequel of our talk at Tokyo-Seoul Conference on Oct 6. These lectures will be fundamental and concrete. We hope that the audience are familiar with basic concepts of finite groups and Hopf algebras. These lectures will be held from Oct 2 to Oct 4, each from 13:30 to 15:00, for a total of 3 lectures. Oct 2 (mon) Introduction to toric code. Oct 3 (tue) Introduction to non-abelian toric code. Oct 4 (wed) Further studies on toric code.
会場: via Zoom / セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Classification of Meromorphic Spin 2-dimensional Conformal Field Theories of Central Charge 24
2023年9月19日(火) 15:00 - 16:30
Möller Sven (Group Leader, Department of Mathematics, University of Hamburg, Germany)
We classify the self-dual (or holomorphic) vertex operator superalgebras (SVOAs) of central charge 24, or in physics parlance the purely left-moving, spin 2-dimensional conformal field theories with just one primary field. There are exactly 969 such SVOAs under suitable regularity assumptions and the assumption that the shorter moonshine module VB^# is the unique self-dual SVOA of central charge 23.5 whose weight-1/2 and weight-1 spaces vanish. Additionally, there might be self-dual SVOAs arising as "fake copies" of VB^# tensored with a free fermion F. We construct and classify the self-dual SVOAs by determining the 2-neighbourhood graph of the self-dual (purely bosonic) VOAs of central charge 24 and also by realising them as simple-current extensions of a dual pair containing a certain maximal lattice VOA. We show that all SVOAs besides VB^# x F and potential fake copies thereof stem from elements of the Conway group Co_0, the automorphism group of the Leech lattice. By splitting off free fermions F, if possible, we obtain the classification for all central charges less than or equal to 24. This is based on joint work with Gerald Höhn (arXiv:2303.17190)
会場: セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
Quasi-BPS categories
2023年9月13日(水) 10:00 - 11:30
戸田 幸伸 (東京大学 カブリ数物連携宇宙研究機構 (Kavli IPMU) 教授)
In this talk, I will explain the notion of "Quasi-BPS category". This is the (yet to be defined) category which categorifies BPS invariants on Calabi-Yau 3-folds, and plays an important role in categorical wall-crossing in Donaldson-Thomas theory. I will explain the motivation of quasi-BPS categories, give definition in the case of symmetric quivers with potential (a local model of CY 3-folds), and their properties. If time permits, I will explain quasi-BPS categories for local K3 surfaces and their relation to derived categories of hyperkahler manifolds. This is a joint work in progress with Tudor Padurariu.
会場: セミナー室 (359号室)
イベント公式言語: 英語
-
セミナー
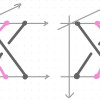
Introduction to braid groups
2023年7月5日(水) 14:00 - 16:30
根上 春 (千葉大学 大学院融合理工学府数学情報科学専攻 博士課程)
Part 1 (14:00-15:00): Introduction to braid groups Braid groups are groups that are defined by figures formed by the entanglement of n strings. Besides this geometric realization, it is a very interesting field where algebra and analysis intersect. In the first half of this seminar, aimed mainly at those unfamiliar with braid groups, we will introduce three aspects of braid groups and review the history of the research. In particular, in the area of its relation to analysis, the relationship between KZ equations and braid groups will be introduced. Part 2 (15:30-16:30): Representations of braid groups and the relationship between monodromy representations of KZ equations In the second half of the talk, after a brief introduction to representation theory, we will introduce the Katz-Long-Moody construction, a method of constructing infinite series of representations of the semi-direct product of braid group and free group. We will also show that its special case is isomorphic to multiplicative middle convolution, a method for constructing monodromy representations of KZ equations. Lastly, we will also discuss the connection between representations of braid groups and knot invariants. The talk includes joint work with Kazuki Hiroe.
会場: セミナー室 (359号室) / via Zoom
イベント公式言語: 英語
117 イベント