Fatgraph models for RNA molecules
- 日時
- 2017年3月23日(木)10:30 - 11:30 (JST)
- 講演者
-
- 藤 博之 (香川大学 教育学部 准教授)
- 言語
- 英語
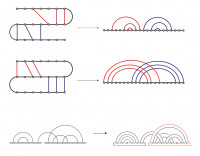
Concepts of fatgraphs and partial chord diagrams occur in many branches of mathematics, including topology, geometry, and representation theory. During the last decade, some applications of these mathematical objects to the research of the molecular biology have been reported. Among them, in particular, a characterization by the genus in the fatgraph presentation of the RNA has been studied remarkably. In this talk, I will explain how the concepts of fatgraphs and partial chord diagrams are applied to the study of the secondary structure of the RNA with pseudoknots, and introduce the matrix model that is invented by basic techniques of the quantum field theory. If time permits, I shall discuss about the matrix model of the protein, and speculate about further developments.
References
- Jørgen Ellegaard Andersen, Hiroyuki Fuji, Robert C. Penner, and Christian M. Reidys, “The boundary length and point spectrum enumeration of partial chord diagrams using cut and join recursion,” Trav. Math. 25 (2017) 213-232, arXiv: 1612.06482 [math-ph]
- Jørgen Ellegaard Andersen, Hiroyuki Fuji, Masahide Manabe, Robert C. Penner, and Piotr Sułkowski, “Partial chord diagrams and matrix models,” Trav. Math. 25 (2017) 233-283, arXiv: 1612.05840 [math-ph]
- Jørgen Ellegaard Andersen, Hiroyuki Fuji, Masahide Manabe, Robert C. Penner, and Piotr Sułkowski, “Enumeration of chord diagrams via topological recursion and quantum curve techniques,” Trav. Math. 25 (2017) 285-323, arXiv: 1612.05839 [math-ph]
