Featured Paper of the Week

27 news

2025-06-04
Featured Paper of the Week

Understanding dynamics and quantum chaos through Krylov space

In everyday life, we often associate chaos with randomness, disorder, or unpredictability—phenomena that appear to lack any discernible pattern. However, from a physics standpoint, understanding chaos requires a more rigorous and precise mathematical framework. In classical physics, chaos is often perceived through its sensitive dependence on initial conditions. Small perturbations in an initial state of a system can lead to vastly different outcomes over time, a behavior commonly known as “butterfly effect”, and typically analyzed within the framework of phase space trajectories, and its detailed topological properties. In contrast, chaos in the quantum realm presents unique challenges. The notion of sharp trajectories in phase space clashes with Heisenberg’s uncertainty principle in quantum mechanics, and initial perturbations cannot be treated in a way that mirrors classical intuition. As a result, quantum chaos requires distinct formulations, relying on diagnostic tools like spectral statistics, out-of-time-order correlators, and entanglement measures. However, the relationships between these different probes are not always clear, and a unified understanding remains an open area of research. In recent years, significant progress has been made in understanding quantum chaos through the lens of operator growth, where localized quantum information encoded in simple operators spreads across a system—a process known as information scrambling. Such phenomena is crucial in understanding the thermalization of a system. Krylov space, a subspace of the operator Hilbert space, provides an elegant framework to describe such operator growth. By decomposing operator dynamics using an orthonormal basis, it traces how simple operators evolve into increasingly complex ones—quantified by a complexity measure in Krylov space. A parallel formulation exists for the evolution of quantum states, offering a complementary perspective. Importantly, to make these ideas applicable to realistic physical scenarios, one must consider open quantum systems—systems that interact with their environment. In such contexts, the dynamics become richer, requiring more generic theoretical and computational techniques. Furthermore, efficient quantum control protocols often leverage the structured Hilbert space, with Krylov subspace methods providing computationally efficient frameworks. These methods facilitate guiding systems along desired adiabatic trajectories, reducing runtime and mitigating decoherence effects, as often required for quantum technologies. These developments form the core focus of this review article.
2020-04-20
Featured Paper of the Week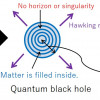

Paper: Black Hole as a Quantum Field Configuration

What's going on inside black holes? The observations to date have taught us the nature of black holes outside and around it, but it does not tell us anything about the inside yet. This is because black holes are "almost" black: gravity is so strong that physical signals from the inside "almost" never come out. So, how can we search for the interior of black holes? It is necessary to return to the basic principles of physics and reconsider what a black hole is. In this paper, we succeeded in describing the inside of black holes based on general relativity and quantum mechanics (quantum field theory). What is important here is a fact that black holes evaporate: According to quantum mechanics, black holes emit weak light, slowly lose energy, and eventually evaporate (Hawking radiation). By taking in this effect from the beginning and analyzing the collapsing process of stars, we obtained the following result: The black hole is a compact object with a surface (instead of horizon) that looks like a conventional black hole from the outside and eventually evaporates without a singularity. (See figure.) Indeed, we explained why this picture can be achieved in quantum field theory. In addition, we investigated how much information is contained inside and showed that the amount (entropy) is given by the surface area. We also described how the energy decreases. This work provides the first field-theoretical formulation of the black hole, and I think it will be the basis for investigating how the information that enters the black hole will go out.
2020-01-24
Featured Paper of the Week

Distance between collapsing matter and trapping horizon in evaporating black holes

How deep can an apple fall into the horizon of a black hole? Of course, in the case of a classic black hole, the apple reaches the center. However, the real world is described by quantum theory, and black holes evaporate by Hawking radiation. This changes the fate of the apple. Negative energy due to vacuum quantum fluctuations is generated near black holes, which enters the black holes and reduces their energy. If there is a horizon, the negative energy will make the horizon smaller. Then, the horizon becomes timelike (while it is null in the classical case). In this paper, we solved approximately the Einstein equation in the vicinity of the horizon and examined the physical (proper) distance between the falling apple and the horizon. It turned out that the distance is a few of the Planck length (due to the exponentially delayed time inside the horizon). This means that essentially no apples fall into the black hole. This result suggest that we should reconsider whether the black hole really has a horizon.
2020-01-09
Featured Paper of the Week

Akizuki-Nakano vanishing theorem and its application for globally F-split 3-folds

In algebraic geometry, it is important to study spaces (=varieties) which may admit singular points. "Smoothing" is an effective way to deal with singularities. Roughly speaking, a smoothing of a (singular) variety helps us to find another variety which is non-singular and is "similar" to the original variety. Namikawa proved that a complex Fano 3-fold whose singular points are at worst ordinary double points admits a smoothing. In this paper, we give an analogy of this result in the case where the Fano variety is not complex, but is defined over a field of positive characteristic. The key ingredient of the proof is the vanishing of the second cohomology of the tangent space, which is a vector space containing an obstruction to construct a smoothing. We prove a positive characteristic analogue of the Akizuki-Nakano type vanishing for 3-dimensional varieties and as a corollary, we conclude the result about a smoothing.
2019-07-22
Featured Paper of the Week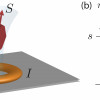

Synthetic dimensions and topological chiral currents in mesoscopic rings

In condensed matter systems, the topological effect of chiral currents is intimately related to two-dimensional systems. Recently emerging concept of "synthetic dimensions" provides a way to explore two-dimensional physics using one dimensional setups by using internal degrees of freedom as an additional dimension. Synthetic dimensions have so far been predominantly developed in atomic and optical physics. In this work, we extend this concept to condensed matter systems of a mesoscopic ring coupled to a nanomagnet. Regarding the spin degrees of freedom of a nanomagnet as a dimension, we interpret a current in the ring, which is locked to the nanomagnet's spin, as chiral edge currents of a two-dimensional quantum Hall system. We thus provide a broader conceptual setting for synthetic dimensions, extending it to a rich domain of potential practical applications in condensed matter systems.
2019-07-16
Featured Paper of the Week

The KO-valued spectral flow for skew-adjoint Fredholm operators

Spectral flow measures the number of eigenvalue crossings of continuous paths of Fredholm operators (which have finite-dimensional kernels). Atiyah, Patodi and Singer first defined spectral flow as a way to study index theory for odd dimensional manifolds. Recent applications of index theory to topological phases, where anti-linear symmetries may occur, have motivated the study of spectral flow on real Hilbert spaces. The paper develops a theory of spectral flow for skew-adjoint Fredholm operators on real Hilbert spaces, which are a classifying space for KO-theory. Our construction applies to bounded and unbounded Fredholm operators, possibly with additional Clifford symmetries, and generalises all previous notions of analytic spectral flow. The results are also relevant to free-fermionic topological phases, where the topological obstruction to two symmetric Hamiltonians having the same strong topological phase can be exactly measured by the KO-valued spectral flow.
2019-07-09
Featured Paper of the Week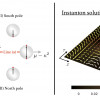

Instantons in Chiral Magnets

More than 50 years ago, Russian physicist Dzyaloshinsky has proposed the specific interaction in some kinds of magnets to explain weak ferromagnetic behavior of them, and soon after that, Professor Moriya has identified its microscopic origin as the spin-orbit coupling. That interaction, now called the Dzyaloshinskii–Moriya (DM) interaction, is one of the most important topics in both experimental and theoretical study of magnetism. This is because it induces novel inhomogeneously ordered states in spin systems such as a chiral soliton lattice and Skyrmion crystal. These interesting states support non-vanishing "topological" charges and have been experimentally observed in some magnetic materials. In this paper, focussing on one-dimensional antiferromagnetic spin chains with the DM interaction, we exhaustively construct instanton solutions with topological excitations and elucidate their properties based on the field theoretical (nonlinear sigma model) description of spin chains. As shown in Fig, the resulting spin configurations show helical ordering due to the DM interaction.
2019-07-04
Featured Paper of the Week

Rigidity of the mod 2 families Seiberg-Witten invariants and topology of families of spin 4-manifolds

After the early 1980s, gauge theory has been used by mathematicians to study 4-dimensional spaces (manifolds). The hottest mathematical subject studied by gauge theory is a sort of difference between the shape of topological (continuous) 4-dimensional manifold and that of smooth 4-dimensional manifold. On the other hand, in most of mathematical areas, it is quite significant to understand symmetry of a given mathematical object, such as a manifold. However, about the space of all symmetries of a 4-dimensional manifold, only few things have been known. In this paper, we study the spaces of symmetries of 4-dimensional manifolds. We revealed that gauge theory (more precisely Seiberg-Witten theory) can extract some difference between the shape of the space of symmetries of a topological 4-dimensional manifold and that of a smooth 4-dimensional manifold. In addition to gauge theory, we also used some classical but deep results in higher-dimensional topology invented 50 years ago. Such a combination of gauge theory with classical results in topology is also a new and interesting direction of this paper.
2019-06-13
Featured Paper of the Week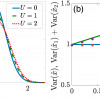

Probing localization and quantum geometry by spectroscopy

Localization has been one of the main topics of interest in condensed matter physics for more than half a century. Study of localizatoin has recently been entering into a new stage because of the developments in the concept of many-body localization, and also of the recent advances in the technology of quantum-engineered systems such as ultracold atoms and trapped ions. In this paper, we propose a novel method to quantitatively study localization of a quantum state in the platform of quantum-engineered systems. Our proposal makes use of the fluctuation-dissipation theorem; we consider periodically modulating the quantum system and observing the exciation rate. We find that the localization of a quantum state is related to the integral of the excitation rate over the modulation frequency. Our proposal to probe localization does not require high resolutino microscopes to spatially resolve the quantum state. We apply our method to various examples which are of direct experimental relevance in ultracold atoms. Moreover, inspired by a relation between quantum fluctuations and the quantum metric, we describe how our scheme can be generalized to extract the full quantum-geometric tensor of many-body systems. The figure (left) shows how the wavefunction of two interacting particles in a harmonic trap spreads as one increases the interaction, and the figure (right) shows how such spreading can be probed through excitation rate measurements for various values of the interaction strengths.
2019-05-28
Featured Paper of the Week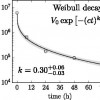

Uncovering critical properties of the human respiratory syncytial virus by combining in vitro assays and in silico analyses

When a virion is left in a liquid medium over some time, it loses its ability to infect cells. This is often because the virion surface proteins become deformed, e.g. because of heat or the ionic content of the medium, such that they can no longer effectively bind cells and infect them. For many viruses (e.g. influenza, HIV and hepatitis C) this loss of infectivity over time follows an exponential. In this paper, we evaluated the rate at which the respiratory syncytial virus (RSV) loses infectivity over time. We were surprised when we found that the loss of infectivity of RSV in our data did not follow an exponential. We used a Weibull distribution to describe the decay and estimated its shape parameter to be k=0.30 [95% credible region: 0.27-0.36], which means the rate of decay gets smaller over time. This is typical of a bad production system wherein a lot of defective products are made which fail soon after production, leaving only well-made products which become defective at a lower rate. In a 2013 paper, Liljeroos and others (doi: 10.1073/pnas.1309070110) showed that as RSV buds from the surface of the cell, bud pinching (closing the bud to free the virion from the cell) is physically difficult, and often leads to misformed buds. The bad structure leads the filamentous (worm-shaped) RSV bud to “plop” outwards (become spherical), flip its surface F proteins (responsible for RSV attachment to host cells) from their pre-trigger (very infectious) to their post-trigger (poorly infectious) state. This is consistent with our finding of k<1, wherein RSV that don’t pinch their bud properly upon cell exit fail (lose infectivity) very early on, and the remaining RSV population which pinched properly will decay following a much less steep exponential.
2019-05-15
Featured Paper of the Week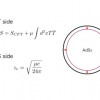

Comments on holographic entanglements in cutoff AdS

AdS/CFT correspondence tells us that a gravity in AdS space is equivalent to CFT which lives on the boundary of the AdS. Recently it has been proposed that an integrable TT deformation of CFTs produces a deformed AdS/CFT. According to the conjecture, the AdS boundary is located at a finite radial cutoff. To investigate the deformed correspondence, we studied holographic entanglement entropy in the cutoff AdS, which is well known as a probe of information theoretic quantity. In particular, we explored its phase transitions. For two-interval entanglement entropy, the transition point monotonically decreases with a deformation parameter, which means that by the TT deformation the degrees of freedom in subsystems are decreasing. Our result implies that the effect of the TT deformation can be regarded as the rescaling of the energy scale.
2019-03-12
Featured Paper of the Week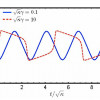

Diffusive Nambu-Goldstone modes in quantum time-crystals

Symmetry and its breaking is one of the most important notions in modern physics. It is known that when a continuum symmetry is spontaneously broken, there appears a gapless excitation called the Nambu–Goldstone (NG) mode. Such a mode appears in several length scales. In the femtometer scale, pions that are responsible for nuclear force, are the NG modes associated with chiral symmetry breaking. In the meter scale, the sound mode in solid is the NG mode associated with spontaneous breaking of translational symmetry. In this paper, we study the NG modes associated with spontaneous breaking of the continuous time-translation symmetry in an open quantum system. For this purpose, we study a system with a van der Pol type nonlinear-friction. By considering small fluctuations around a time-periodic mean-field solution, we find that a gapless collective mode, which is a diffusive one, necessarily appears; this is nothing but the NG mode of a time crystal. We also show that noncommutative breaking of the time-translation and U(1) symmetries results in mixing of the NG modes, and the (typically) propagating NG mode appears.
2019-03-06
Featured Paper of the Week

Paper: Non-sinusoidal Waveform in Temperature-Compensated Circadian Oscillations

We have autonomous daily rhythm in our body, so-called “circadian clock” for which we can wake up without alarm clock. The rhythm governs the timing of physiological events such as hormone secretion. Curiously, the period of our daily rhythms is stable to temperature, a phenomenon known as “temperature compensation.” Temperature compensation has been a mystery for many years because underlying reaction processes tend to accelerate with temperature. If our internal clock was sensitive to temperature, the clock would not function properly any more. To uncover the mystery, we developed a simpler model of circadian clock based on experimental evidences whilst many realistic simulators have been proposed. Using the model, we derived the period formula. The formula states that “the more non-sinusoidal, the longer period.” From the formula, we predicted that more non-sinusoidal waveform at higher temperature should be observed in reality which is necessary to cancel out the period shortening effect at higher temperature. Unexpectedly, we obtained a similar period formula for a limit cycle oscillation of electrical circuit (van der Pol model), indicating that non-sinusoidal waveform lengthens period. How can circadian clock and electrical circuit behave similarly? We wish to understand the reason in a future.
2019-02-07
Featured Paper of the Week

Quantum annealing for polynomial systems of equations

The advent of Noisy Intermediate-Scale Quantum (NISQ) quantum computers has galvanized efforts towards discovering near-term applications. An algorithm for solving polynomial systems of equations was proposed by Dr. Chang (iTHEMS) in collaboration with Dr. Gambhir (Lawrence Livermore National Lab), Dr. Humble (Oak Ridge National Lab), and Dr. Sota (R-CCS) and implemented a linear solver on a D-Wave quantum annealer. While the problems are currently limited to sizes that are easily solved by classical computers, the team showed that the quantum algorithm exhibits constant scaling with increasing condition number, in direct contrast with classical methods. Additionally, the quantum algorithm may also be applied iteratively to exponentially decrease the relative residual, allowing for the classical solution to be reproduced by the quantum computer to single precision. However, the scaling with problem size is unfortunately exponentially bad, reflecting limitations of current quantum computers. Fortunately, there is a great amount of interest and effort put fourth by the greater quantum annealing community geared towards tackling this problem, including using inhomogeneous driving fields, reverse annealing, and even hardware developments towards universal quantum annealers.
2019-01-31
Featured Paper of the Week

Back Reaction of 4D Conformal Fields on Static Geometry

In classical mechanics, a black hole is described by a vacuum solution with the horizon of the Einstein equation. For spherical case, it is the Schwarzschild metric, and the location of the horizon is given by the Schwarzschild radius. (Note that the Schwarzschild radius can also be defined even for a star without horizon.) In quantum mechanics, a black hole evaporates and information inside it seems to be lost, which is contradict to the principle of quantum mechanics. An effective way to address this problem is to consider again “What is the black hole in quantum mechanics?” In this paper, we examined how robust the use of the Schwarzschild metric to represent a black hole is in quantum mechanics. We consider conformal matters (e.g. electromagnetic field) and introduce the quantum effect (4D conformal anomaly) into the Einstein equation, which necessarily makes the equation non-vacuum. We start from the Schwarzschild metric, add the quantum effect perturbatively, and solve the Einstein equation in a self-consistent manner. Then, we showed that the quantum effect can play a crucial role in shaping the static geometry near the Schwarzschild radius. The geometry depends on a parameter corresponding to a boundary condition, and the existence of the horizon requires the fine-tuning. Therefore, in quantum mechanics, a typical static spherical solution does not have a horizon.
2019-01-22
Featured Paper of the Week

Index theory and topological phases of aperiodic lattices

The paper studies the interactions between dynamical systems, represented via groupoid operator algebras, and index theory, described using Kasparov's bivariant K-functor. The key motivating example is the dynamical systems associated to Delone sets. Delone sets give a model of aperiodic atomic configurations, where the material may be amorphous or quasi-crystalline. The atomic configuration does not have a group structure, but key properties can be encoded in a discrete groupoid. We construct bivariant K-cycles, a generalisation of K-theory classes, that encode the dynamics of the aperiodic lattice. For the case of quasi-crystalline configurations, we obtain finer information coming from the long-range aperiodic order of the material. We then use our constructed K-cycles to define bulk topological phases of aperiodic materials. A bulk-boundary correspondence is also shown, which arises from factorisation properties of the constructed K-cycles.
2018-11-30
Featured Paper of the Week

Engaging the Public with Supernova and Supernova Remnant Research Using Virtual Reality

On April 21, 2018, residents of Wako came to RIKEN for the Open Day. Over one hundred people visited the exhibit of the Astrophysical Big Bang Laboratory (ABBL) and interacted with real scientific data using virtual reality (VR). With the help of the entire ABBL and several students from Rikkyo U, people as young as 2 and as old as 80 got to explore a supernova remnant in 3-D, as if it was in the room with them. (A supernova remnant results from the explosion of a star; ABBL does numerical simulations to understand the explosion mechanism.) In this report, Gilles Ferrand (ABBL/iTHEMS) and Don Warren (iTHEMS) explain what makes VR exciting to explore your data and communicate your research, and how to make your own VR booth at next year's Open Day — or any other event! We are happy to discuss this exhibit, and answer any questions you have, at a coffee meeting, wine meeting, or another occasion.
2018-11-12
Featured Paper of the Week

Gamow-Teller transitions from high-spin isomers in $N=Z$ nuclei

Atomic nuclei are composed of protons and neutrons. We may imagine like a certain number of (quantum) balls putting in a (self-bound) container. On the one hand, the nuclear magic numbers show the single-particle features of nuclei; On the other hand, the giant resonances show the emergent collective features. For example, an intuitive image of giant dipole resonance is: All protons form a group while all neutrons form another group, and these two groups oscillate against to each other collectively. Gamow-Teller resonance is an important kind of giant resonances involving not only the spin but also the isospin degrees of freedom in nuclei. So far, most, if not all, of experimental and theoretical studies on this direction focus on the resonances from the nuclei being in their ground states, largely due to the experimental limitations. However, it is expected that, in the near future, our world-leading nuclear facility in RIKEN can generate high-quality radioactive beams with nuclei being in their high-spin isomeric states. Motived by this perspective, we predict that the Gamow-Teller transitions from the high-spin isomers could be much more collective than the corresponding transitions from their ground states, by taking nuclei 52Fe and 94Ag as examples. This would be one of the promising collaborations between theorists and experimentalists in RIKEN.
2018-11-02
Featured Paper of the Week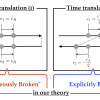

Effective field theory of time-translational symmetry breaking in nonequilibrium open system

Although we know "all things are in a state of flux. (Patna rhei.)", it has been still an interesting question whether we have "universal" features in such time-evolution of all things. Considering the non-equilibrium open systems like the Brownian particles, we have tackled this problem from the point of view of time-translational symmetry. We regard the transient diffusive (or time-oscillating) behaviors as "symmetry-broken phases of matter", and develop a way to describe their spacetime evolution. Our formalism is based on the so-called effective field theory (EFT) originally developed in the context of particle physics and now used in almost every branches of physics. The advantage of the EFT is that it enables us to capture the possible universal properties in the large-scale (low-energy) behaviors of systems. As a result, we find the existence of the Nambu-Goldstone-like mode during transient time-evolution, which gives the universal diffusive behaviors of all things in a state of flux.
2018-10-18
Featured Paper of the Week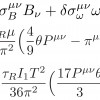

Non-equilibrium Chiral Magnetic/Vortical Effects in Viscous Fluids

Chiral magnetic and vortical effects are novel effects in quantum fluids with chiral anomaly. We utilize the chiral kinetic theory in a relaxation-time approximation to investigate the nonlinear anomalous responses of chiral fluids with viscous effects. Unlike the cases in equilibrium, it is found that the chiral magnetic effect and chiral vortical effect are modified by the shear and bulk strengths. Particularly, the shear strength could result in charged Hall currents for chiral magnetic and chiral vortical effects, which propagate perpendicular to applied magnetic fields and vorticity. These quantum corrections stemming from side jumps and anomalies are dissipative and pertinent to interactions.
2018-10-09
Featured Paper of the Week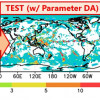

Online Model Parameter Estimation With Ensemble Data Assimilation in the Real Global Atmosphere

When and where will it rain, and how heavy? – this is a central question that meteorology tries to address. Numerical weather prediction (NWP) is a major approach using data assimilation with mathematical models to predict the weather. The NWP models discretize the earth atmosphere into 3-dimensional grids, and compute the evolution of the atmospheric states based on physical processes (e.g., fluid dynamics, radiation, and water phase changes). The NWP models cannot include subgrid-scale and complex processes explicitly, and these complex phenomena are represented by simplified equations so-called “parameterization”. Parameterization usually contains tunable model parameters, and manual tuning of these parameters is a tedious but important task. This study explores an objective and autonomous approach to optimizing these parameters using data assimilation. We chose a parameter of the subgrid-scale parameterization of raindrop initiation processes of a global NWP model. We successfully mitigated the overproduced precipitation of the NWP model by estimating the model parameter with satellite-observed precipitation data. Figure: Global precipitation forecasts (mm 6h-1) at 0000 UTC on 16 June 2014 by an NWP model. (left) control experiment with the default model setting, (middle) test experiment with the model parameter estimation, and (right) satellite observation, respectively. Overproduced precipitation over ocean in the control experiment is successfully mitigated by the model parameter estimation.
2018-10-01
Featured Paper of the Week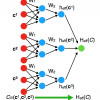

Self-learning Monte Carlo method with Behler-Parrinello neural networks

Self Learning Monte-Carlo (SLMC) method is one of the recent promising applications of machine learning techniques to computational physics especially Marcov-Chain Monte-Carlo (MCMC) simulations in statistical physics systems. In SLMC, we prepare an effective Hamiltonian with tunable coupling constants and try to reproduce the value of the real Hamiltonian by adjusting the coupling constants. This procedure corresponds to the supervised machine learning. After the learning, we employ it for global updates in MCMC, and it drastically reduces the autocorrelation, i.e. similarity of configurations in the Marcov-Chain, thanks to the local structure of the effective Hamiltonian. In our paper, we present two novel techniques for SLMC in a quantum Monte-Carlo simulation. First technique is the use of neural networks. Based on the neural net architecture by Behler and Parrinello in the context of molecular dynamics machine learning, we develop how to construct general purposed effective Hamiltonian for SLMC. Second contribution is a new proposal for regularization in SLMC that we call batch-atom normalization. It is a generalization of the well-known technique in deep learning, and we observe it drastically improve the learning procedure for effective Hamiltonian represented by neural network.
2018-09-19
Featured Paper of the Week

The relative Mishchenko--Fomenko higher index and almost flat bundles

Existence of a positive scalar curvature (PSC) metric has been one of the central topics in differential topology of higher dimensional manifolds. Index theory provides a topological invariant whose vanishing is an effective necessary condition of the existence of a PSC metric. Recently, Chang-Weinberger-Yu introduce a new index theoretic invariant called the relative higher index detecting the non-existence of a PSC metric on spin manifolds with boundary. The aim of this paper is to understand this invariant from Riemannian gemetric point of view. Firstly, we introduce a new definition of the relative higher index and prove that it is equivalent to the existing definitions. Secondly, by using our new definition, we relate the relative higher index with a Riemannian geometry of vector bundles; the index pairing with almost flat vector bundles. This is a relative analogue of the theory of Gromov-Lawson for closed spin manifolds.
2018-08-28
Featured Paper of the Week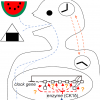

Two Ck1δ transcripts regulated by m6A methylation code for two antagonistic kinases in the control of the circadian clock

Thanks to the accumulation of molecular knowledges about biological clock, we can predict a missing link “X” in the system by using a realistic simulator. Meal-time is known to influence our sleep-wake timing. But the mechanism has been unknown. This time, the group of Dr. Okamura at Kyoto University discovered a new enzyme (named, Ck1δ2) that possibly links between our metabolic system and biological clock. Based on the experimental results by Dr. Okamura, two iTHEMS members (Gibo and Kurosawa) predicted the specific biochemical process, activated by the new enzyme. The prediction was conducted by using a 190 variables model with all genes and proteins. Fortunately, the prediction was confirmed experimentally. The point for the prediction was the activation of the new enzyme “slowed” the biological clock in the experiment while the activation of most enzymes “accelerate” the clock in the simulator. Now, the mechanism is studied by using a simpler model. Then, a possible scenario is that amino-acids in our food influence our sleep-wake timing via the new enzyme.
2018-07-30
Featured Paper of the Week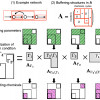

Structural Bifurcation Analysis in Chemical Reaction Networks

In living cells, large numbers of chemical reactions form complicated networks (e.g. metabolic networks). It is considered that dynamics arising from such networks are the origin of biological functions. In this study, we developed a theoretical method to analyze bifurcation properties, i.e. properties of structural changes of steady-state solutions, from topology of reaction networks. Such a topological approach is advantageous because reaction kinetics is not well known in detail. Specifically, we showed that a reaction network can be decomposed into subnetworks based on a certain topological criteria, and showed that any bifurcation point is associated with a particular subnetwork ((3) in the figure). Further, we identified the parameters inducing bifurcations ((4) in the figure) and chemical concentrations exhibiting bifurcating behaviors ((5) in the figure). Our method is particularly useful to study large networks, since it allows us network decomposition. Biologically, bifurcation properties are related with plasticity of living systems, i.e. qualitative changes of physiological states induced by environmental conditions or gene-expressions. Our result suggests that biological plasticity arises from network topology.
2018-07-23
Featured Paper of the Week
Hilbert schemes of two points on K3 surfaces and certain rational cubic fourfolds

The goal of birational geometry is the classification of algebraic varieties up to birational equivalence. An algebraic variety is called rational if it is birationally equivalent to the projective space. In this paper, Genki Ouchi studied the rationality problem of (complex) cubic fourfolds, that is four dimensional complex hypersurface defined by a polynomial of degree 3. Conjecturelly, very general cubic fourfolds are irrational. However, no cubic fourfold has been proven to be irrational so far. On the other hand, there are five known examples of rational cubic fourfolds. They expect that the mysterious relation between rational cubic fourfolds and K3 surfaces is a key to solve the rationality problem. There are two inconsistent conjectures about it. So they should modify one of them at least. Together with previous works, he proved that known rational cubic fourfolds satisfy both conjectures. To modify the conjectures, we have to find a new rational cubic fourfold.
2018-07-17
Featured Paper of the Week

Production of intense episodic Alfvén pulses: GRMHD simulation of black hole accretion disks

The episodic dynamics of the magnetic eruption of spinning black hole (BH) accretion discs and the associated intense shape-up of their jets are studied via three-dimensional general-relativistic magnetohydrodynamics (GRMHD). The embedded magnetic fields in the disc are amplified by a magnetorotational instability (MRI) so large as to cause an eruption of the magnetic field (reconnection) and large chunks of matter accrete episodically toward the roots of the jets upon such an event. We also find that the eruption events produce intensive Alfvén pulses, which propagate through the jets. After the eruption, the disc returns to the weakly magnetic state. Such disc activities cause short-time variabilities in mass accretion rate at the event horizon, as well as electromagnetic luminosity inside the jet. Since the dimensionless strength parameter a0 = eE/m_eωc of these Alfvén wave pulses is extremely high for a substantial fraction of Eddington accretion rate accretion flows on to supermassive black holes, the Alfvén shocks turn into ultrarelativistic (a0 >> 1) bow wake acceleration, manifesting as ultra-high-energy cosmic rays and electrons, which finally emit gamma-rays. Since our GRMHD model has universality in its spatial and temporal scales, it is applicable to a wide range of astrophysical objects, ranging from active galactic nuclei (AGNs, the primary target of this research) to micro-quasars. Properties such as the time variabilities of blazar gamma-ray flares and the spectrum observed by the Fermi Gamma-ray Observatory are explained well by linear acceleration of electrons by a bow wake. Figure caption: A snap shot of accreting gas onto a spinning black hole and Poynting flux dominated jet formation by 3-dimensional general relativistic magneto-hydrodynamic simulation. Log-scaled inverse of plasma beta (magnetic pressure / thermal pressure) (x-y plane), mass density (y-z plane), and magnetic pressure (x-z plane) are shown.

27 news