Self-learning Monte Carlo method with Behler-Parrinello neural networks

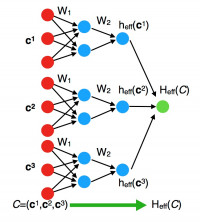
Self Learning Monte-Carlo (SLMC) method is one of the recent promising applications of machine learning techniques to computational physics especially Marcov-Chain Monte-Carlo (MCMC) simulations in statistical physics systems. In SLMC, we prepare an effective Hamiltonian with tunable coupling constants and try to reproduce the value of the real Hamiltonian by adjusting the coupling constants. This procedure corresponds to the supervised machine learning. After the learning, we employ it for global updates in MCMC, and it drastically reduces the autocorrelation, i.e. similarity of configurations in the Marcov-Chain, thanks to the local structure of the effective Hamiltonian. In our paper, we present two novel techniques for SLMC in a quantum Monte-Carlo simulation. First technique is the use of neural networks. Based on the neural net architecture by Behler and Parrinello in the context of molecular dynamics machine learning, we develop how to construct general purposed effective Hamiltonian for SLMC. Second contribution is a new proposal for regularization in SLMC that we call batch-atom normalization. It is a generalization of the well-known technique in deep learning, and we observe it drastically improve the learning procedure for effective Hamiltonian represented by neural network.