Structural Bifurcation Analysis in Chemical Reaction Networks

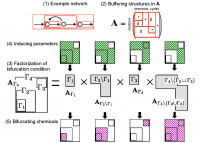
In living cells, large numbers of chemical reactions form complicated networks (e.g. metabolic networks). It is considered that dynamics arising from such networks are the origin of biological functions. In this study, we developed a theoretical method to analyze bifurcation properties, i.e. properties of structural changes of steady-state solutions, from topology of reaction networks. Such a topological approach is advantageous because reaction kinetics is not well known in detail. Specifically, we showed that a reaction network can be decomposed into subnetworks based on a certain topological criteria, and showed that any bifurcation point is associated with a particular subnetwork ((3) in the figure). Further, we identified the parameters inducing bifurcations ((4) in the figure) and chemical concentrations exhibiting bifurcating behaviors ((5) in the figure). Our method is particularly useful to study large networks, since it allows us network decomposition. Biologically, bifurcation properties are related with plasticity of living systems, i.e. qualitative changes of physiological states induced by environmental conditions or gene-expressions. Our result suggests that biological plasticity arises from network topology.