Math Seminar by Dr. Wataru Kai on March 22, 2021

On March 22, the last iTHEMS Math seminar in FY 2020 was held. This time, we invited Wataru Kai from Tohoku University.

The title of the talk was “The Green-Tao theorem for number fields”. The main topic of the talk was his recent joint work with his collaborators about the Green-Tao theorem and its generalization.

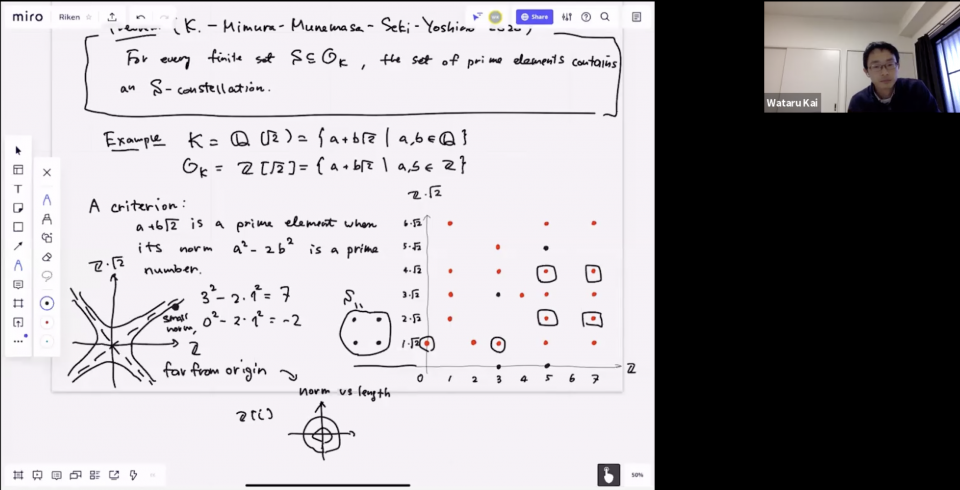
In the first part, he explained the historical background and the technology behind the proof of the Green-Tao theorem, which asserts that there are arbitrarily long arithmetic progressions of prime numbers. In the second part, he introduced algebraic numbers and algebraic integers, which generalize rational numbers and integers, respectively, and he explained how we can generalize the Green-Tao theorem to this situation. For example, if we think of numbers of the form a+b\sqrt{5}, these are algebraic numbers. Plotting them on the ab-plane, each of the numbers corresponds to a lattice point. We can draw a “shape” by choosing finite number of those lattices. Then, the generalized Green-Tao theorem asserts that, by applying scaling and parallel translation, we can make all of the chosen lattice points correspond to prime elements simultaneously. Here, prime element is a generalization of prime number in the world of algebraic numbers. He also explained that at some point of the proof of the generalized Green-Tao theorem, a classical technique well-known to algebraic number theorists plays a fundamental role.

Reported by Hiroyasu Miyazaki