Math-Phys Joint Seminar by Toshihiro Ota on October 2, 2020

On October 2, Toshihiro Ota gave a talk at the iTHEMS Math-Phys Joint Seminar. His whole talk was on the interrelation among integrable lattIce models, quiver gauge theories, and hidden TQFT structure.

His first talk was a sort of lecture on TQFT and integrable lattice model at an elementary level. At the beginning of the first talk, he explained quantum mechanics (QM). Then as a variant of QM, he introduced an axiomatic definition of topological quantum field theory as a special class of quantum field theory. He also introduced lattice model which can be seen as a discrete version of quantum field theories. In particular, he mentioned the integrability of the 1-dimensional Ising model.

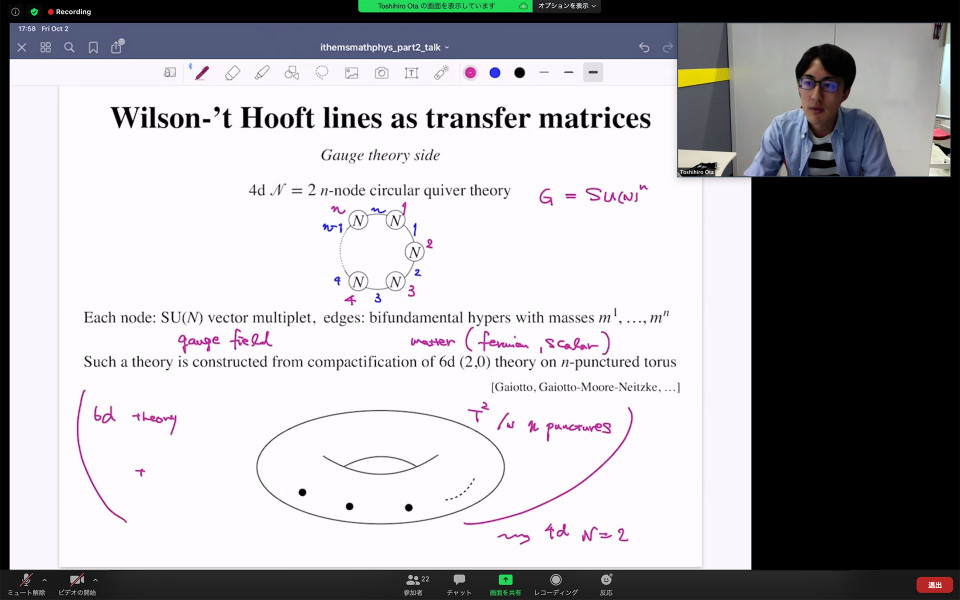
In the second talk, he focused on the correspondence between Wilson-'t Hooft lines in a class of quantum gauge theories and transfer matrices in the corresponding integrable lattice models. At first, he gave an explanation of “classical integrability” and “quantum integrability” for field theories. In the case of 2-dimensional lattice model, he explained that the integrability is described by the Yang-Baxter equation. Then he moved on to the details of the correspondence. In the lattice model side of the correspondence, he described the transfer matrix in terms of n-copies of L-operators. Moreover, in order to compare to the gauge theory side, he took the trigonometric limit and rewrote the transfer matrix by “more fundamental” L-operators. The gauge theory side is in particular given by 4d N=2 n-node circular quiver theory. The theory is defined on a 4d twisted spacetime S^1 xε R^2 x R, and he gave an expression of the Wilson-'t Hooft line wrapping the circle S^1. As the main result of his joint work with Kazunobu Maruyoshi and Junya Yagi, he gave a relation between these Wilson-’t Hooft lines and transfer matrices. Finally, he gave several comments related to integrability from TQFT in extra dimension.