Volume 154
Back to Newsletter List
Event Schedule
Events for the 3rd week of June 2021
2021-06-10
Friday, June 18, 12:30- Coffee Meeting
Friday, June 18, 16:00- iTHEMS Math Seminar
Seminar Report
iTHEMS Biology Seminar by Dr. Yingying Xu on June 3, 2021
2021-06-07
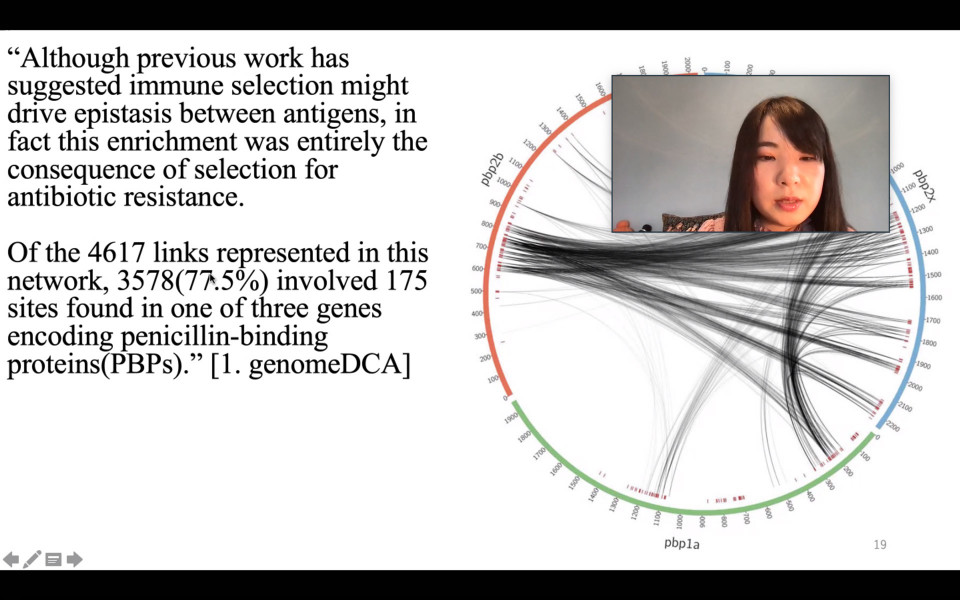
On June 3rd, Yingying Xu who recently joined iTHEMS gave a talk at the Biology Seminar. She spoke about her past research on applying ideas from statistical physics to genetics, especially on what is called "epistasis". Statistics plays a crucial role in the study of genetics, and one of the main challenges now is to understand the combined effect of multiple mutations, which is often referred to as epistasis. This clearly requires input from statistical physics, so I was very excited to hear the progress made with people from statistical physics - Yingying and her colleagues being involved. Her talk was also very helpful for everyone to get an idea of how advanced statistics/mathematics is being applied to genetics. It was also great to see the expertise of Yingying, and we will be looking forward to further interaction with her.
Reported by Jeffrey Fawcett
An overview of genome-wide epistasis and co-selection analysis
June 3 (Thu) 10:00 - 11:00, 2021
Upcoming Events
Seminar
iTHEMS Math Seminar
Stable eigenvalues of compact anti-de Sitter 3-manifolds
June 18 (Fri) 16:00 - 18:10, 2021
Kazuki Kannaka (Special Postdoctoral Researcher, RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS))
Geometric objects that have been investigated in detail so far, such as closed Riemann surfaces, are sometimes locally homogeneous. Loosely speaking, their infinitesimal behavior is the same at each point. In this talk, I would like to explain the idea of investigating such objects using the Lie group theory.In the first part of the talk, I will recall the notions of Lie group actions and their quotient spaces with examples, and then explain the definitions of locally homogeneous spaces and their deformations (Teichmüller spaces). In the second part of the talk, I will consider anti-de Sitter manifolds as a special case, i.e., Lorentzian manifolds of negative constant curvature. As in the Riemannian case, a differential operator called the Laplacian (or the Klein-Gordon operator) is defined on Lorentzian manifolds. Unlike the Riemannian case, it is no longer an elliptic differential operator but a hyperbolic differential operator. In its spectral analysis, new phenomena different from those in the Riemannian case have been discovered in recent years, following pioneering works by Toshiyuki Kobayashi and Fanny Kassel. I would like to explain stable eigenvalues of the hyperbolic Laplacian of anti-de Sitter 3-manifolds with recent progress.
Venue: via Zoom
Event Official Language: English
Seminar
Information Theory Seminar
Introduction to the replica method
June 23 (Wed) 13:30 - 15:40, 2021
Yoshiyuki Kabashima (Professor, Graduate School of Science, The University of Tokyo)
The replica method is a mathematical technique for evaluating the "quenched" average of logarithm (or a real number power) of the partition function with respect to predetermined random variables that condition the objective system.
The technique has a long history, dating back at least to a book by Hardy et al in 1930s, but has become well known only since its application to the physics of spin glasses in 1970s. More recently, its application range is spreading rapidly to various fields in information science, including information theory, communication theory, signal processing, computational complexity theory, machine learning, etc.
In this talk, we introduce the basic idea of the replica method and its mathematical fault illustrating a few examples.
*Detailed information about the seminar refer to the email.
Venue: via Zoom
Event Official Language: English
Seminar
DMWG Seminar
Precise WIMP Dark Matter Abundance and Standard Model Thermodynamics
June 24 (Thu) 16:30 - 17:30, 2021
Satoshi Shirai (Project Assistant Professor, Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU), The University of Tokyo)
We are now living in the era of precision cosmology. The relic abundance of dark matter (DM) is now observationally well-determined, and its error is smaller than O(1)%. This means that the same or much higher precision is required when we make theoretical predictions.
Weakly Interacting Massive Particle (WIMP) has long been the leading candidate for DM because of its beautiful mechanism to predict the observed relic abundance. WIMP is in the same thermal bath as the Standard Model particles in the beginning. At a certain point when the temperature of the Universe is smaller than the DM mass, it decouples to fix its number density. The yield of the DM is determined by its annihilation cross-section to the Standard Model sector.
It seems that there is no ambiguity in the calculation of this process at first: the cross-section is purely theoretical and all the remainings are described in the Standard Model physics. However, the source of the uncertainty does remain in the Standard Model sector. The dilution of the number density of DM particle depends on the expansion rate of the Universe, which is determined by the Standard Model particles. The effective degree of freedom (d.o.f) of the relativistic species controls this factor. We have to deal with the non-equilibrium dynamics to precisely describe the time-evolution of the d.o.f, in which we need numerical approaches.
In this talk, he introduced his work to update these calculations. By implementing the latest findings in the non-equilibrium dynamics in i) the neutrino decoupling, ii) the QCD phase transition, iii) the electroweak phase transition, and iv) the perturbative calculations, they found that the final d.o.f is smaller than the previous estimate in more than 1%. This is larger than the level of precision in observations. It is also important that the uncertainty is quantified by them.
Another good news is that he makes the calculated d.o.f with its error publically available. With these updates, we now correctly know the points to probe DM!
Venue: via Zoom
Event Official Language: English
Seminar
iTHEMS Math Seminar
An introduction to modular functions, conformal field theories, and moonshine phenomena
July 2 (Fri) 16:00 - 18:10, 2021
Mizuki Oikawa (Junior Research Associate, RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS) / Student Trainee, RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS) / Ph.D. Student, Graduate School of Mathematical Sciences, The University of Tokyo)
Moonshine phenomena are certain mysterious connections between modular functions and finite groups. The first example is the celebrated monstrous moonshine, which connects the J-invariant and the Monster group. Surprisingly, this relationship can be well understood in terms of chiral conformal field theory. In this talk, I would like to explain what is chiral conformal field theory and how it gives moonshine phenomena.
In the first part of the talk, the notion of modular function will be introduced and the precise statement of the monstrous moonshine will be given. Then the monstrous moonshine will be explained in terms of vertex operator algebra, a mathematical model of chiral conformal field theory.
In the second part of the talk, we focus on the question: what is chiral conformal field theory mathematically? In addition to vertex operator algebras, other mathematical models of chiral conformal field theory, namely conformal nets and Segal conformal field theories, will be introduced. Recent progress on the relationship among these three models, including the Carpi--Kawahigashi--Longo--Weiner correspondence and the geometric realization of conformal nets will also be reviewed.
Venue: via Zoom
Event Official Language: English
Colloquium
iTHEMS Colloquium
Quantitative Population Dynamics in Interdisciplinary Biology
July 8 (Thu) 10:30 - 12:00, 2021
Shingo Iwami (Professor, Graduate School of Science, Nagoya University)
Through the course of life, from the moment of birth till death, an organism will achieve various states of equilibrium or ‘homeostasis’ which will inevitably encounter perturbations. The processes of cell growth, differentiation, infection, mutation, evolution and adaptation work together as a coordinated ‘system’, described by mathematical models for population dynamics, to maintain a healthy state. Any disruptions to this system leads to disease including infection, allergy, cancer, and aging. We are conducting interdisciplinary research to elucidate “Quantitative Population Dynamics” through the course of life with original mathematical theory and computational simulation, which are both our CORE approach. Our mathematical model-based approach has quantitatively improved a current gold-standard approach essentially relying on the statistical analysis of “snapshot data” during dynamic interaction processes in life sciences research. In this talk, I will explain how our interdisciplinary approach extends our understanding for complicated clinical data and apply real world problem with an example of the Novel Coronavirus Disease, COVID-19.
Venue: via Zoom
Event Official Language: English
If you would like to cancel your subscription or change your email address,
please let us know via our contact form.
Copyright © iTHEMS, RIKEN. All rights reserved.