iTHEMS Colloquium by Prof. Kenji Fukaya on April 16, 2021
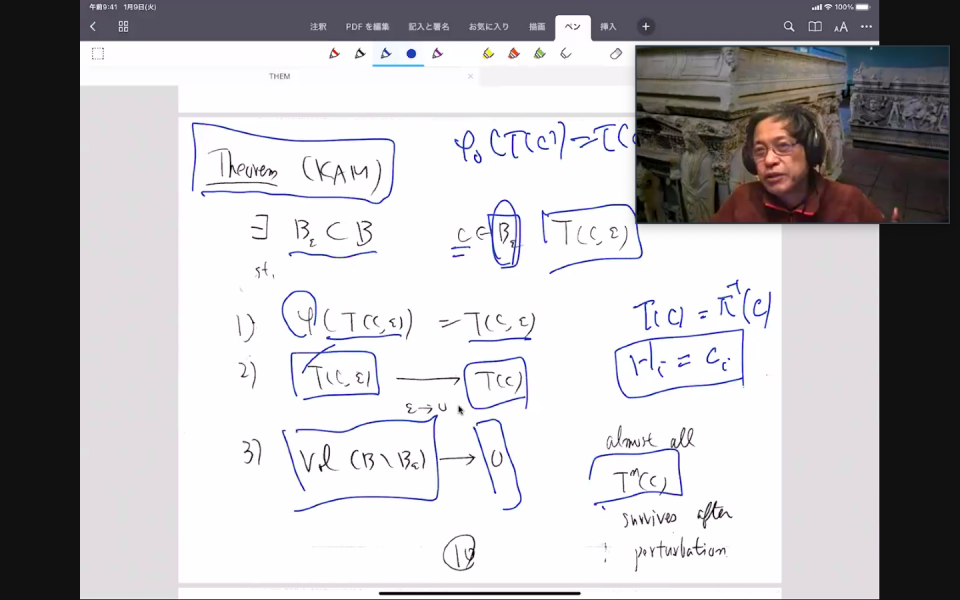
On April 16, 2021, 13:30-15:00 (JST) 0:30-2:00(EDT), Professor Kenji Fukaya, Simons Center for Geometry and Physics, Stony Brook University, gave a colloquium talk by zoom. The title was "Mirror symmetry and KAM theory". His talk began at the origin of symplectic geometry, namely, the Hamiltonian dynamics. He reviewed completely integrable Hamiltonian systems, where the first integrals define foliation by half dimensional Lagrangian tori with linear flows. The KAM (Kolmogorov-Arnold-Moser) theory describes perturbation of this system and shows that almost all tori persist. Then Professor Fukaya explained the Lagrangian torus fibration found by Strominger-Yau-Zaslow, with the example of the complex projective space. For the complex projective n-space, the image of the moment map is an n-simplex and the regular fibers are Lagrangian n-tori. The inverse image of the boundary of the simplex corresponds to the singular fiber of the holomorphic fibration (the product of homogeneous coordinates) to a disk, By choosing a symplectic form, around the singular fiber of holomorphic fibration, there is defined the monodromy map by using the Hamiltonian flow of the Hamiltonian function that is the absolute value of the fibering. Professor Fukaya told that for this example in dim n = 2, the monodromy near the singular fiber exhibits the KAM theoretic behavior, but in dim n = 3, it is not the case with respect to the Fubini-Study symplectic form. However, he expects it can be the case with respect to the Calabi-Yau Kaehler form. This correspondence between symplectic manifolds (the torus fibration of the complex projective space) and complex manifolds (the holomorphic map to the disk) is an introductory example of the mirror symmetry. His talk might enter much deeper part related with homological mirror symmetry, but he stopped and concluded by saying that the KAM theory explains the transition from completely integrable systems to chaos and it should be possible to find alternative in mirror symmetry or field theory which will explain the transition from stable system to chaos. The talk of Professor Fukaya was really stimulating and his enthusiasm impressed the audience.
Reported by Takashi Tsuboi